BeagleBone Black with Ubuntu
Introduction
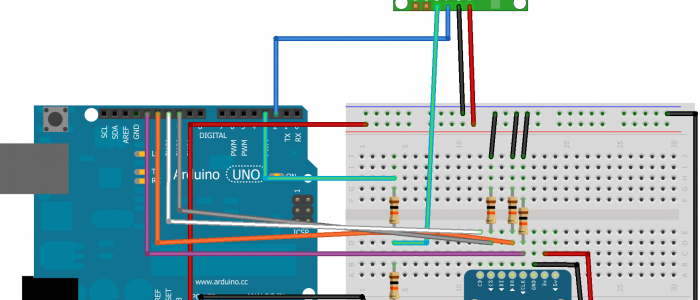
The BeagleBone Black is a very powerful and affordable microcontroller - superior to an Arduino Uno in a lot of ways. It's fast enough to be used as a desktop computer, yet it has more pinouts than an Uno. With the BeagleBone Black priced at $45, it's really a great value compared to an Arduino ($35) or even a Raspberry Pi ($35).
An Arduino, while power-efficient and reliable, is incapable of high performance use cases like image processing. Even the ARM based Arduino Due is thousands of times slower than the BeagleBone Black. It can't even parse a JPEG (the library won't fit in the flash). A BeagleBone or Raspberry Pi, however, can easily process live streams from USB webcams and OpenCV.
 The BeagleBone Black is significantly faster and more capable than the comperable $35 Raspberry Pi Model B. Both have the same RAM, HDMI out, and Ethernet, but the BeagleBone Black has superior IO (more and faster) and has a faster processor capable of running Ubuntu, where the Raspberry Pi cannot due to its older architecture. Remember, Raspberry Pi was intended to be an educational tool to teach kids to program, not to help you hack together a robot. The BBB has two extra processors dedicated to effectively manage the pinouts.
The BeagleBone Black is significantly faster and more capable than the comperable $35 Raspberry Pi Model B. Both have the same RAM, HDMI out, and Ethernet, but the BeagleBone Black has superior IO (more and faster) and has a faster processor capable of running Ubuntu, where the Raspberry Pi cannot due to its older architecture. Remember, Raspberry Pi was intended to be an educational tool to teach kids to program, not to help you hack together a robot. The BBB has two extra processors dedicated to effectively manage the pinouts.
The downside? The pre-installed OS (Angstrom) at this point in time will break if you do a package upgrade. Not only will it never boot again once it finishes updating, but it also uses too much of the /tmp/ filesystem and stalls halfway though. You can run Ubuntu on it, but there isn't much of a point, since it's basically incapable of having a desktop UI or using OpenGL as far as I can tell. There's no reason why it shouldn't be possible. In fact, LXDE and XFCE sort of work. This leads to the bigger problem. The documentation, support, and community behind BeagleBone is nowhere near that of the Raspberry Pi, let alone Arduino (which has the best by far).