PD Feedback Control Introduction
PD Feedback Control IntroductionUses
A PD controller can be used in a real-time on a robot where a goal value can be both measured and controlled. A PD control is robust, which means that it can overcome unexpected behavior.
For example, a PD controller could be used in the cruise control on a car. The driver decides the goal speed and the controller in the car could see how fast the car is going, since cars have a speedometer. Under ideal conditions, all it would take to maintain speed is to keep the engine throttled at a predetermined constant amount. However, many unforseable factors can change how much gas is needed to maintain speed. For example, the quality of the gas, engine temperature, road incline, and wind speed. A controller needs to be able to overcome these unpredictable or difficult to measure sources of error to maintain a given speed and accelerate or decellerate as needed.
Premise
PD stands for proportion and derivative.
- Multiplying a constant (kp) to the "error" - or the difference between the desired and current values - will pull the output towards the desired value. A larger proportion constant means faster responses.
- Multiplying another constant (kd) to the rate of change in the error essentially says "slow down before you get there". It keeps the system from vibrating by anticipating the error. More anticipation means less vibration.
Analogy
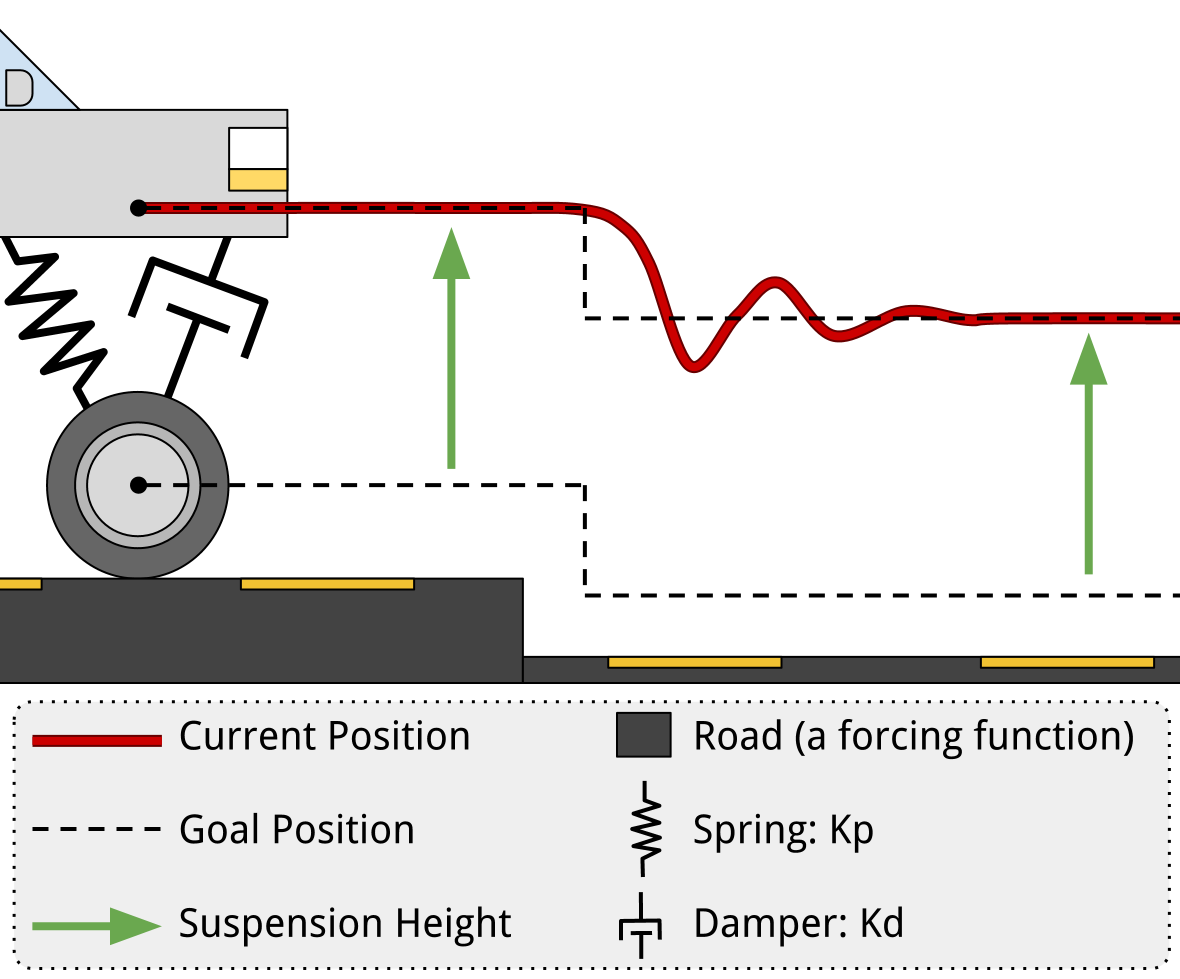
Cars have shock absorbers and springs on each of their wheels. The springs try to keep the car a certain distance off the ground. This is like the proportion in a PD controller, but usually this "error" distance is zero. The shock absorber on a car is a damper, which helps the car to stop vibrating from the springs - just like the derivative portion of a PD controller.
The similarity between the suspension system and a PD controller is due to the spring and damper pairing. Obviously, it is not exactly a control system. Rather, if you visualize the position graphs in terms of current position and goal position, you begin to see how a PD controller will behave.
Just like this suspension system controls the hight of a car based on the position of its tire, you can robustly control just about anything your robot has the ability to both affect and sense. It does not have to be a position. For example, you could control the temperature of an oven as long as you have control of the heating element and have a temperature sensor inside the oven.
An Example Problem
So, lets say you have a motor and an encoder that allows you to read the position of the motor. You want the motor to go to a goal position of your choosing. This motor is attached to a vertical rack and pinion so that the graph is easy to visualize.
Bad Solution
You could say "if you're not there, go towards the goal", like this Arduino code:
if ( position < goal ) { // too low
goUp(); // set direction
analogWrite(motor, 255); // go full speed
}
else if ( position == goal ) { // at goal
analogWrite(motor, 0); // stop
}
else if ( position > goal ) { // too high
goDown(); // set direction
analogWrite(motor, 255); // go full speed
}
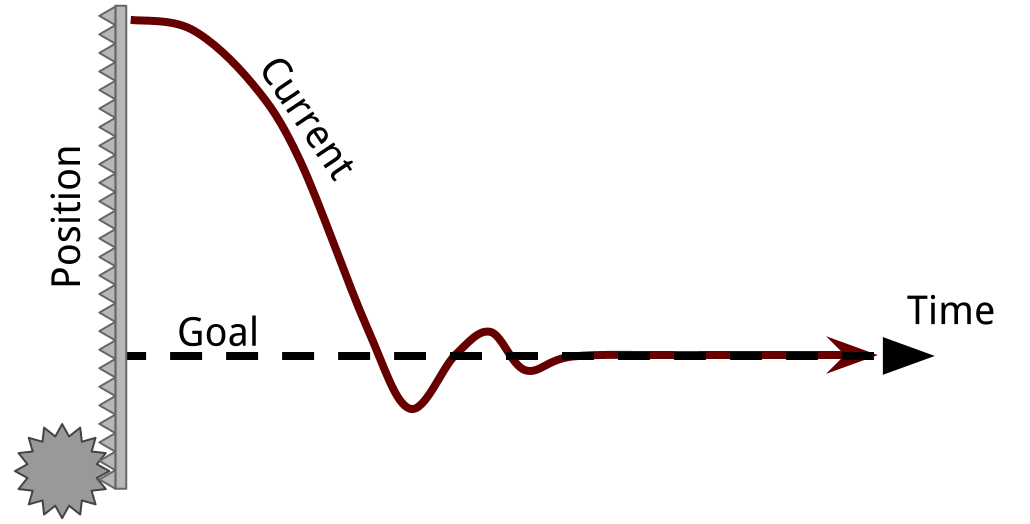
 The problem here is that many times the system will have sufficient momentum to keep going even though there is no more current and no force being applied by the motor. Unless there is sufficient friction, you will overshoot the goal. If this happens once, it'll probably happen on the next pass too - resulting in vibration. This is obviously undesirable since the system never rests at the goal position, wastes energy, and will wear down unecessarily.
The problem here is that many times the system will have sufficient momentum to keep going even though there is no more current and no force being applied by the motor. Unless there is sufficient friction, you will overshoot the goal. If this happens once, it'll probably happen on the next pass too - resulting in vibration. This is obviously undesirable since the system never rests at the goal position, wastes energy, and will wear down unecessarily.
Good Solution
Now lets simply change the code on the Arduino microcontroller to use a PD control.
// the PD controller requires speed be calculated
int output = Kp*(goal-position) - Kd*speed
if ( output >= 0 ) { // positive
goUp(); // set direction
analogWrite(motor, output); // go partial speed
}
else { // negative goDown(); // set direction analogWrite(motor, -output); // go partial speed }
Note that this new PD control requires the speed, not just the position. This is not usually a problem, since a microcontroller is usually pretty good at keeping time. You can simply keep track of the change in position divided by the change in time. This requires a little more code on the Arduino.
unsigned long now = micros(); // store the current time in "now"
// change in position over change in time
speed = ( position - lastPosition ) / ( now - lastTime )
// this measurement is now the previous one
lastPosition = position;
lastTime = now;
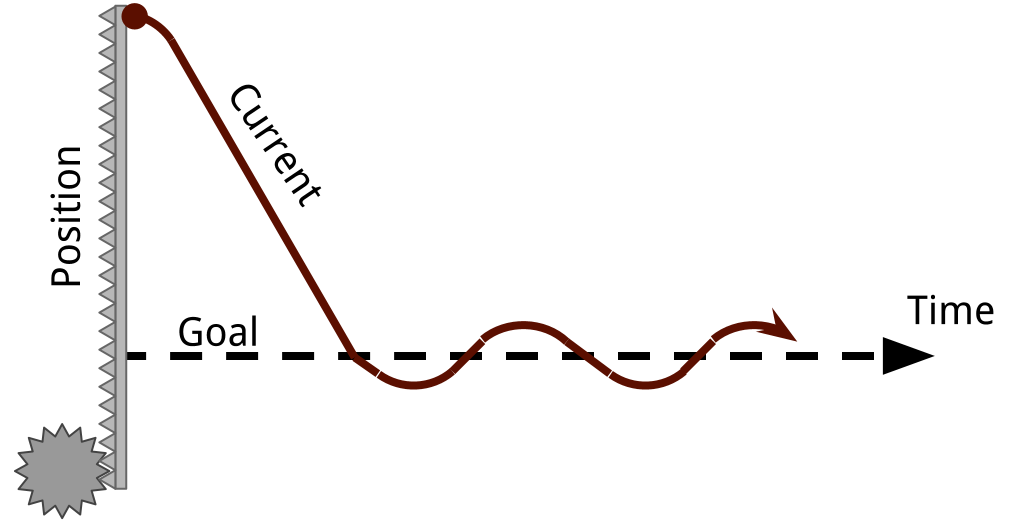
Depending on the values that you pick for the variables Kp and Kd, you could get two different kinds of behaviors: damped vibration (left), or a critically/over damped system (right).
Choosing Values
Picking the right Kp and Kd values is important. To some extent, you can just do it by trial and error.
| Desired Result | Change |
|---|---|
| Get There Fast (low rise time) | Smaller Kp |
| Less Overshoot | Smaller Kp, Larger Kd |
| Less Vibration | Larger Kd |
It is no exagguration to say that there is a science to picking the right parameters, though. They can actually be precisely chosen by using math. Essentially, you need to be able to describe what you are controlling with an equation to make a transfer function, then find the characteristic equation. It's actually a lot easier than it sounds.